Tengo una nueva petición de ayuda respecto al uso de Solver, en este caso se requiere minimizar una función bajo unas condiciones dadas. El planteamiento de este problema de optimización lineal es:
Como siempre al querer emplear Solver lo más importante es la construcción de nuestro sistema de ecuaciones, esto es, de nuestras condiciones y función objetivo.
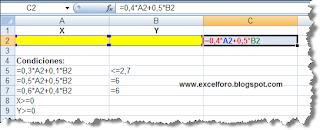
Para lo que dispondremos de dos celdas A2, B2 como variables a obtener o celdas cambiantes; y en el rango A5:A7 las restricciones definidas.
Vemos que en la celda C1 hemos añadido la función objetivo a minimizar:
=0,4*A2+0,5*B2
de acuerdo al enunciado de nuestro problema.
Las restricciones o condiciones dadas que incluiremos en la hoja de cálculo serán entonces:
Además de estas restricciones incluiremos en la ventana diálogo de la herramienta Solver dos más que asegurarán que tanto una variable como la otra, es decir, A2 y B2 sean mayores o iguales que cero.
Una vez planteado todo nuestro problema en la hoja de cálculo, podemos navegar y ejecutar Solver; desde la Ficha Datos > Análisis > Solver:
Importante haber marcado mínimo valor de la celda objetivo.
Sólo queda 'Resolver', con lo que obtendremos un resultado minimizado de la función objetivo de 5,40 cumpliendo todas las restricciones.
| ...tengo estas funciones las quiero resolver por medio del solver en excel y me gustaria que me ayudes claro si puedes :D minimizar Z = 0.4 X1 + 0.5 X2 sujeto a 0.3 X1 + 0.1 X2 (MENOR IGUAL QUE) 2.7 0.5 X1 + 0.5 X2 =6 0.6 X1 + 0.4 X2 = 6 X1 (MAYOR IGUAL QUE) 0 X2 (MAYOR IGUAL QUE) 0... |
Como siempre al querer emplear Solver lo más importante es la construcción de nuestro sistema de ecuaciones, esto es, de nuestras condiciones y función objetivo.
Para lo que dispondremos de dos celdas A2, B2 como variables a obtener o celdas cambiantes; y en el rango A5:A7 las restricciones definidas.
Vemos que en la celda C1 hemos añadido la función objetivo a minimizar:
=0,4*A2+0,5*B2
de acuerdo al enunciado de nuestro problema.
Las restricciones o condiciones dadas que incluiremos en la hoja de cálculo serán entonces:
- en la celda A5
=0,3*A2+0,1*B2 - en la celda A6
=0,5*A2+0,5*B2 - en la celda A7
=0,6*A2+0,4*B2
Además de estas restricciones incluiremos en la ventana diálogo de la herramienta Solver dos más que asegurarán que tanto una variable como la otra, es decir, A2 y B2 sean mayores o iguales que cero.
Una vez planteado todo nuestro problema en la hoja de cálculo, podemos navegar y ejecutar Solver; desde la Ficha Datos > Análisis > Solver:
Importante haber marcado mínimo valor de la celda objetivo.
Sólo queda 'Resolver', con lo que obtendremos un resultado minimizado de la función objetivo de 5,40 cumpliendo todas las restricciones.



No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.