Toca analizar hoy un gráfico estadístico importante: Gráfico Cajas y Bigotes.
En esta ocasión explicaré cómo construirlo de una manera muy simple empleando la versión de Excel 2016.
Este gráfico de Cajas y Bigotes muestra en un solo gráfico las diferentes magnitudes estadísticas básicas, empleadas en los estudios de estadística descriptiva.
Hablamos en concreto de:
Mínimo: función =MIN(rango_celdas)
Cuartil 1 (al 25%): función =CUARTIL.INC(rango_celdas;1)
Mediana o cuartil 2 (al 50%): función =CUARTIL.INC(rango_celdas;2)
Cuartil 3 (al 75%): función =CUARTIL.INC(rango_celdas;3)
Máximo: función =MAX(rango_celdas)
Media aritmética: función =PROMEDIO(rango_celdas)
Rango (intervalo valores): fórmula =MAX-MIN
Lo que vamos a conseguir es ver de la siguiente forma estos datos:
Veámoslo con un ejemplo.
Disponemos de estas tres variables en el rango de celdas B1:C14:
Construir el gráfico es sencillo.
Seleccionamos el rango B1:B14 y desde la Ficha Insertar > grupo Gráficos > botón Insertar gráfico de estadística > Cajas y Bigotes.
Con el gráfico ya construido, y mostrando casi todas las variables, empezamos a configurarlo.
1-eliminamos el título del gráfico
2-eliminamos las etiquetas del eje horizontal
3-añadimos la Leyenda en la parte inferior
4-agregamos las etiquetas de datos.
Un paso importante para reflejar la información es hacer doble clic sobre las distintas series de datos para acceder al Formato de serie de datos y así definir las Opciones de serie, desde donde nos aseguraremos de marcar la opción de cálculo de los cuartiles al que nos interesa, en mi caso Mediana inclusiva.
La implicación de esta elección responde a:
*Mediana inclusiva:= La mediana se incluye en el cálculo si el número de valores de los datos fuera impar.
*Mediana exclusiva:= La mediana se excluye del cálculo si el número de valores de los datos es impar.
Otras posibilidades son las de incorporar los puntos intermedios, incluir las medias, añadir la linea que uno los puntos medios o de especial relevancia Mostrar valores atípicos.
Para entender el concepto de valor atípico deberemos tener ciertas nociones estadísticas y en particular del conocido como Rango Intercuartil (IQR en inglés). Dato que se calcula como diferencia del cuartil 3 y el cuartil 1.
A la pregunta de a qué distancia de la media del 50% de datos distribuidos entre esos cuartiles puede situarse un valor y aún ser considerado como un valor 'razonable' o 'atípico', los estadísticos llegaron al acuerdo en que (IQR * 1.5) puede utilizarse para establecer un margen superior e inferior razonable.
De tal forma que serían atípicos por debajo aquellos valores inferiores a:
=cuartil_1-(IQR x 1,5)
y serían atípicos por encima o superiores a:
=cuartil_3+(IQR x 1,5)
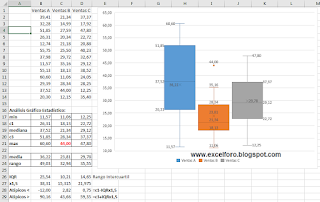
En nuestro ejemplo hemos calculado todas las magnitudes estadísticas en el rango A16:D29, como se veían en la imagen anterior.
Si nos centramos, a modo de ejemplo, en los valores de la serie de 'Ventas B' verificamos los cálculos:
Nos fijaremos que hay un valor en la serie (valor= 44) que aparece reflejado como 'Atípico', y fuera por tanto del rango de estudio... notemos que en dicha serie el valor máximo es el valor anterior 35,16 (NO atípico).
Este comportamiento está altamente relacionado con el tipo de cálculo del cuartil seleccionado.
En esta ocasión explicaré cómo construirlo de una manera muy simple empleando la versión de Excel 2016.
Este gráfico de Cajas y Bigotes muestra en un solo gráfico las diferentes magnitudes estadísticas básicas, empleadas en los estudios de estadística descriptiva.
Hablamos en concreto de:
Mínimo: función =MIN(rango_celdas)
Cuartil 1 (al 25%): función =CUARTIL.INC(rango_celdas;1)
Mediana o cuartil 2 (al 50%): función =CUARTIL.INC(rango_celdas;2)
Cuartil 3 (al 75%): función =CUARTIL.INC(rango_celdas;3)
Máximo: función =MAX(rango_celdas)
Media aritmética: función =PROMEDIO(rango_celdas)
Rango (intervalo valores): fórmula =MAX-MIN
Lo que vamos a conseguir es ver de la siguiente forma estos datos:
Veámoslo con un ejemplo.
Disponemos de estas tres variables en el rango de celdas B1:C14:
Construir el gráfico es sencillo.
Seleccionamos el rango B1:B14 y desde la Ficha Insertar > grupo Gráficos > botón Insertar gráfico de estadística > Cajas y Bigotes.
Con el gráfico ya construido, y mostrando casi todas las variables, empezamos a configurarlo.
1-eliminamos el título del gráfico
2-eliminamos las etiquetas del eje horizontal
3-añadimos la Leyenda en la parte inferior
4-agregamos las etiquetas de datos.
Un paso importante para reflejar la información es hacer doble clic sobre las distintas series de datos para acceder al Formato de serie de datos y así definir las Opciones de serie, desde donde nos aseguraremos de marcar la opción de cálculo de los cuartiles al que nos interesa, en mi caso Mediana inclusiva.
La implicación de esta elección responde a:
*Mediana inclusiva:= La mediana se incluye en el cálculo si el número de valores de los datos fuera impar.
*Mediana exclusiva:= La mediana se excluye del cálculo si el número de valores de los datos es impar.
Otras posibilidades son las de incorporar los puntos intermedios, incluir las medias, añadir la linea que uno los puntos medios o de especial relevancia Mostrar valores atípicos.
Para entender el concepto de valor atípico deberemos tener ciertas nociones estadísticas y en particular del conocido como Rango Intercuartil (IQR en inglés). Dato que se calcula como diferencia del cuartil 3 y el cuartil 1.
A la pregunta de a qué distancia de la media del 50% de datos distribuidos entre esos cuartiles puede situarse un valor y aún ser considerado como un valor 'razonable' o 'atípico', los estadísticos llegaron al acuerdo en que (IQR * 1.5) puede utilizarse para establecer un margen superior e inferior razonable.
De tal forma que serían atípicos por debajo aquellos valores inferiores a:
=cuartil_1-(IQR x 1,5)
y serían atípicos por encima o superiores a:
=cuartil_3+(IQR x 1,5)
En nuestro ejemplo hemos calculado todas las magnitudes estadísticas en el rango A16:D29, como se veían en la imagen anterior.
Si nos centramos, a modo de ejemplo, en los valores de la serie de 'Ventas B' verificamos los cálculos:
Nos fijaremos que hay un valor en la serie (valor= 44) que aparece reflejado como 'Atípico', y fuera por tanto del rango de estudio... notemos que en dicha serie el valor máximo es el valor anterior 35,16 (NO atípico).
Este comportamiento está altamente relacionado con el tipo de cálculo del cuartil seleccionado.





Como se cambia las unidades mayores y menores en estos gráficos?
ResponderEliminarEs decir la escala a la que aparecen los números en el eje y?
ResponderEliminarHola Ignacio, cómo estás?
EliminarUn placer saludarte igualmente.
Pues lamentablemente este gráfico no ofrece está opción de eje (que otros sí)... a cambio aporta otras características novedosas.
Un cordial saludo
No es posible graduar el eje horizontal con el nombre de cada serie?
ResponderEliminarHola Jorge, cómo estás?
EliminarUn placer saludarte igualmente.
Pues lamentablemente este gráfico no ofrece está opción de eje (que otros sí)... a cambio aporta otras características novedosas.
Un cordial saludo