Aplicaremos hoy la herramienta Solver para solucionar un problema muy típico.
¿cuál es la ruta más corta entre dos puntos?.
Para esto analizaremos el Algoritmo de Dijkstra (lee algo más en Wikipedia)
Nuestro punto de partida es conocer la distribución de los puntos y distintos nodos intermedios entre el Inicio y el Final del camino.
Para nuestro ejemplo tomaremos el siguiente mapa:
Lo más importante ahora, puesto que vamos a aplicar la herramienta Solver es plantear un modelo correcto.
Detallamos, paso a paso, cada uno de las posibles combinaciones para avanzar por las distintas rutas.
Así, manualmente, comenzando desde el punto de Inicio detallamos cada punto, y así sucesivamente en cada nodo:
Inicio => A
Inicio => B
Inicio => C
A => D
A => C
B => C
B => E
C => D
C => E
D => Final
E => Final
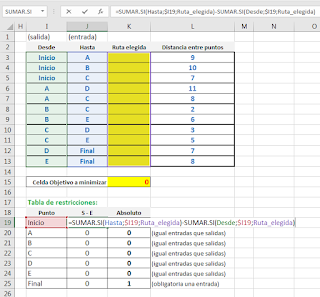
Lo vemos trasladado a nuestra hoja de cálculo:
Para facilitar el trabajo he asignado nombres definidos a los rangos de trabajo:
Desde =Ruta!$I$3:$I$13
Distancia_entre_puntos =Ruta!$L$3:$L$13
Hasta =Ruta!$J$3:$J$13
Ruta_elegida =Ruta!$K$3:$K$13
Concretamos en la celda K15 la que será nuestra función objetivo:
=SUMAPRODUCTO(Ruta_elegida;Distancia_entre_puntos)
Dicha celda será en Solver nuestra celda a minimizar.
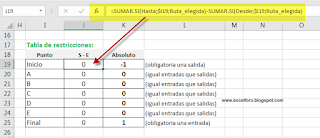
Finalmente, para completar nuestro modelo, incorporamos un rango donde disponer las restricciones. En estas restricciones se debe verificar que en cada nodo intermedio el número de entradas sea igual al de salidas, excepto al punto de Inicio y punto Final que solo de salir y entrar una única vez.
Este se consigue sumando los valores que devolverá Solver en K3:K13 (serán nuestras celdas cambiantes).
la fórmula empleada en este rango de restricciones, que recoge la idea es:
=SUMAR.SI(Hasta;$I19;Ruta_elegida)-SUMAR.SI(Desde;$I19;Ruta_elegida)
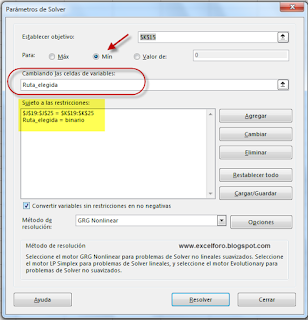
Completado nuestro modelo en la hoja de cálculo, estamos en disposición de lanzar Solver:
En nuestra ventana diálogo indicamos nuestra intención de minimizar la celda K15 (con la fórmula SUMAPRODUCTO, como se indicaba más arriba); para lo cual permitimos modificar el valor de las celdas K3:K13 (a la que habíamos asignado el nombre 'Ruta_elegida').
Además añadimos dos restricciones:
1- que los valores a completar en K3:K13 solo pueden ser ceros y uno (binarios).
2- que el rango J19:J25 (resta formulada de Entradas menos Salidas) sea tras el cálculo igual a los valores de K19:K25 (con valores que representan el neto en cada punto o nodo).
Tras presionar el botón de Resolver obtenemos, para nuestro ejemplo, la siguiente solución:
Concluyendo que la ruta más óptima es la que recorre:
Inicio - Nodo C - Nodo D - Final
con una distancia mínima de 17.
¿cuál es la ruta más corta entre dos puntos?.
Para esto analizaremos el Algoritmo de Dijkstra (lee algo más en Wikipedia)
Nuestro punto de partida es conocer la distribución de los puntos y distintos nodos intermedios entre el Inicio y el Final del camino.
Para nuestro ejemplo tomaremos el siguiente mapa:
Lo más importante ahora, puesto que vamos a aplicar la herramienta Solver es plantear un modelo correcto.
Detallamos, paso a paso, cada uno de las posibles combinaciones para avanzar por las distintas rutas.
Así, manualmente, comenzando desde el punto de Inicio detallamos cada punto, y así sucesivamente en cada nodo:
Inicio => A
Inicio => B
Inicio => C
A => D
A => C
B => C
B => E
C => D
C => E
D => Final
E => Final
Lo vemos trasladado a nuestra hoja de cálculo:
Para facilitar el trabajo he asignado nombres definidos a los rangos de trabajo:
Desde =Ruta!$I$3:$I$13
Distancia_entre_puntos =Ruta!$L$3:$L$13
Hasta =Ruta!$J$3:$J$13
Ruta_elegida =Ruta!$K$3:$K$13
Concretamos en la celda K15 la que será nuestra función objetivo:
=SUMAPRODUCTO(Ruta_elegida;Distancia_entre_puntos)
Dicha celda será en Solver nuestra celda a minimizar.
Finalmente, para completar nuestro modelo, incorporamos un rango donde disponer las restricciones. En estas restricciones se debe verificar que en cada nodo intermedio el número de entradas sea igual al de salidas, excepto al punto de Inicio y punto Final que solo de salir y entrar una única vez.
Este se consigue sumando los valores que devolverá Solver en K3:K13 (serán nuestras celdas cambiantes).
la fórmula empleada en este rango de restricciones, que recoge la idea es:
=SUMAR.SI(Hasta;$I19;Ruta_elegida)-SUMAR.SI(Desde;$I19;Ruta_elegida)
Completado nuestro modelo en la hoja de cálculo, estamos en disposición de lanzar Solver:
En nuestra ventana diálogo indicamos nuestra intención de minimizar la celda K15 (con la fórmula SUMAPRODUCTO, como se indicaba más arriba); para lo cual permitimos modificar el valor de las celdas K3:K13 (a la que habíamos asignado el nombre 'Ruta_elegida').
Además añadimos dos restricciones:
1- que los valores a completar en K3:K13 solo pueden ser ceros y uno (binarios).
2- que el rango J19:J25 (resta formulada de Entradas menos Salidas) sea tras el cálculo igual a los valores de K19:K25 (con valores que representan el neto en cada punto o nodo).
Tras presionar el botón de Resolver obtenemos, para nuestro ejemplo, la siguiente solución:
Concluyendo que la ruta más óptima es la que recorre:
Inicio - Nodo C - Nodo D - Final
con una distancia mínima de 17.





Muchas Gracias
ResponderEliminarHola Ismael te puedo plantear una variante en este caso ?
ResponderEliminarHola,
Eliminarcuál es esa variante al método?
Slds
Mi consulta es como hallar la menor distancia entre N rutas donde pase por todos los nodos contemplando que no todas las rutas pasan por todos los nodos,
ResponderEliminarHola,
Eliminarparece más un problema de combinatoria, donde listar posibles rutas.
En todo caso no está claro si esas N rutas deben pasar por todos los nodos o no?
Slds
No necesariamente
ResponderEliminarPor ejemplo:
ResponderEliminarruta 1: cliente 1 - 2 - 3- 4
ruta 2: cliente 2-3-5
ruta 3: cliente 4-2-1
ruta 4: cliente 5-1-2
buscar cuales son las rutas mas cortas que atienden todos los clientes
ResponderEliminaren este caso podrían ser: ruta 1+ 2 o ruta 1+3
que atienden los clientes (1-2-3-4-5)
Cómo se podría resolver mediante solver?
ResponderEliminarHola,
Eliminarla cuestión es que Solver precisamente realiza ese proceso de optimización, pero no lo refleja o lo deja grabado en ningún sitio, salvo el resultado óptimo final.
Creo que , insistiendo un 'poco' es un problema de combinatoria, por lo que en mi opinión Solver no es la herramienta apropiada
Slds
Muchas gracias Ismael. Saludos
ResponderEliminar