Me he dado cuenta que últimamente solo escribo de lenguaje M (es mi pequeño vicio)... pero hay que liberar la cabeza con otras heerramientas :D
En esta ocasión os planteo generar un código con Office Scripts que recorra las distintas hojas de un libro, buscando las 'Tablas' que hubiera en cada hoja, para finalmente trasladar el resultado a una sola hoja 'Resumen', con los valores anexados...
Lo que viene siendo un clásico de la programación.
Me parece un código interesante por que emplea las sentencias más habituales como condicionales o bucles entre las colecciones de hojas o celdas... Una recopilación de los diferentes artículos publicados sobre el tema en este blog.
Vamos con el código.
Aprovechando que hace poco se liberó la ficha 'Automatizar' en la versión de escritorio, y que este código será 100% compatible con la versión Web, emplearemos la opción.
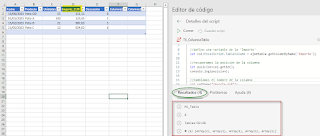
En la Ficha 'Automatizar' buscaremos el botón de 'Nuevo Script', lo que nos abrirá el panel de Editor de código donde escribiremos nuestro código...
No hay grandes diferencias entre esta pestaña de la versión de escritorio con la de la versión web.
En el editor de código escribiremos:
Las etapas del proceso están explicadas/comentadas...
Lo interesante es que la filosofía o la idea detrás del código coincide con la que podrías aplicar con código VBA 😊...
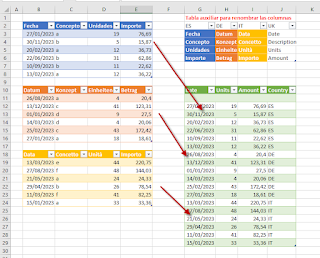
Y el resultado es el esperado.
Mencionar algunas propiedades y métodos del objeto Tabla para Office Scripts... algunos empleados en el Script anterior.
Nos adentramos en el interface de ExcelScript.Table!!
La verdad es que es difícil decidir cuál de los muchos métodos y propiedades mostrar (existen algo más de cuarenta!! :O), asi que iré a los clásicos.
addTable(range, true/false): Creamos una tabla nueva con o sin encabezado.
addColumn(index, values, name): Agrega una nueva columna a la tabla.
addRow(index, values) Agrega una fila a la tabla.
delete() Elimina la tabla.
deleteRowsAt(index, count) Elimine un número especificado de filas en un índice determinado.
getHeaderRowRange() Obtiene el objeto de intervalo asociado a la fila de encabezado de la tabla.
getName() Nombre de la tabla.
getRange() Obtiene el objeto de rango asociado a toda la tabla.
getRangeBetweenHeaderAndTotal() Obtiene el objeto de rango asociado al cuerpo de datos de la tabla.
getRowCount() Obtiene el número de filas de la tabla.
getTotalRowRange() Obtiene el objeto de intervalo asociado a la fila de totales de la tabla.
resize(newRange) Cambie el tamaño de la tabla al nuevo intervalo. El nuevo intervalo debe superponerse con el intervalo de tabla original y los encabezados (o la parte superior de la tabla) deben estar en la misma fila.
setName(name) Nombre de la tabla.
Unos ejemplos de esto sería el siguiente código:
El resultado previo a eliminar la tabla (último paso) es:
Ten presente que para trabajar a nivel de columnas deberás, en algunas ocasiones, hacer uso del interface ExcelScript.TableColumn!!!
Por suerte los métodos y propiedades en este caso son solo diez ;-)
delete() Elimina la columna de la tabla.
getFilter() Recupera el filtro aplicado a la columna.
getHeaderRowRange() Obtiene el objeto de rango asociado a la fila de encabezado de la columna.
getId() Devuelve una clave única que identifica la columna de la tabla.
getIndex() Devuelve el número de índice de la columna dentro de la colección de columnas de la tabla. Indizado con cero.
getName() Especifica el nombre de la columna de tabla.
getRange() Obtiene el objeto de rango asociado a toda la columna.
getRangeBetweenHeaderAndTotal() Obtiene el objeto de rango asociado al cuerpo de datos de la columna.
getTotalRowRange() Obtiene el objeto de rango asociado a la fila de totales de la columna.
setName(name) Especifica el nombre de la columna de tabla.
Además de los métodos concretos dentro de ExcelScript.Table como pueden ser:
getColumn(key) Obtiene un objeto de columna por nombre o identificador. Si la columna no existe, este método devuelve undefined.
getColumnById(key) Obtiene un objeto de columna por identificador. Si la columna no existe, devolverá undefined.
getColumnByName(key) Obtiene un objeto de columna por Name. Si la columna no existe, devolverá undefined.
getColumns() Representa una colección de todas las columnas de la tabla.
y del ya comentado
addColumn(index, values, name): Agrega una nueva columna a la tabla.
Un ejemplo lo podemos ver en el siguiente código:
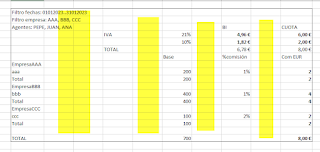
El efecto del trabajo lo vemos en la imagen siguiente:
Espero sirva como breve introducción al trabajo con tablas en nuestras hojas de cálculo con Office Scripts.
En esta ocasión os planteo generar un código con Office Scripts que recorra las distintas hojas de un libro, buscando las 'Tablas' que hubiera en cada hoja, para finalmente trasladar el resultado a una sola hoja 'Resumen', con los valores anexados...
Lo que viene siendo un clásico de la programación.
Me parece un código interesante por que emplea las sentencias más habituales como condicionales o bucles entre las colecciones de hojas o celdas... Una recopilación de los diferentes artículos publicados sobre el tema en este blog.
Vamos con el código.
Aprovechando que hace poco se liberó la ficha 'Automatizar' en la versión de escritorio, y que este código será 100% compatible con la versión Web, emplearemos la opción.
En la Ficha 'Automatizar' buscaremos el botón de 'Nuevo Script', lo que nos abrirá el panel de Editor de código donde escribiremos nuestro código...
No hay grandes diferencias entre esta pestaña de la versión de escritorio con la de la versión web.
En el editor de código escribiremos:
function main(workbook: ExcelScript.Workbook) {
let hojas = workbook.getWorksheets();
let encab: string[][] = [['Fechas', 'País', 'Producto', 'Unidades']];
console.log ('num columnas ' + encab[0].length);
console.log('num filas ' + encab.length);
let arrFin:string[][] = []; //array 2D - dos dimensiones
//bucle por todas las hojas del libro
hojas.forEach(hoja => {
let tablas=hoja.getTables(); //identificamos las tablas de cada hoja
//bucle por las tablas
tablas.forEach(tbl => {
//trabajamos con todos los datos de la tabla (sin encabiezados ni fila totales)
let colsUds=tbl.getRangeBetweenHeaderAndTotal().getValues();
//filtramos solo los registros cuyo valoe en Unidades > 50 (columna 4 = 3 en base cero)
//el resultado es otra ARRAY
//let filtrado = colsUds.every( valor => valor[3] < 50); //alternativa a .filter
let filtrado = colsUds.filter( valor => valor[3] > 50);
//anexamos-agregamos cada nueva array a las anteriores
arrFin = [].concat(arrFin,filtrado);
})
});
console.log (encab);
console.log (arrFin);
//devuelvo la matriz filtrada a la hoja REsultado
let rdo=workbook.getWorksheet("Resultado")
rdo.getRange("A1:D1").setValues(encab);
rdo.getRange("A2:D" + (arrFin.length+1)).setValues(arrFin);
};Las etapas del proceso están explicadas/comentadas...
Lo interesante es que la filosofía o la idea detrás del código coincide con la que podrías aplicar con código VBA 😊...
Y el resultado es el esperado.
Mencionar algunas propiedades y métodos del objeto Tabla para Office Scripts... algunos empleados en el Script anterior.
Nos adentramos en el interface de ExcelScript.Table!!
La verdad es que es difícil decidir cuál de los muchos métodos y propiedades mostrar (existen algo más de cuarenta!! :O), asi que iré a los clásicos.
addTable(range, true/false): Creamos una tabla nueva con o sin encabezado.
addColumn(index, values, name): Agrega una nueva columna a la tabla.
addRow(index, values) Agrega una fila a la tabla.
delete() Elimina la tabla.
deleteRowsAt(index, count) Elimine un número especificado de filas en un índice determinado.
getHeaderRowRange() Obtiene el objeto de intervalo asociado a la fila de encabezado de la tabla.
getName() Nombre de la tabla.
getRange() Obtiene el objeto de rango asociado a toda la tabla.
getRangeBetweenHeaderAndTotal() Obtiene el objeto de rango asociado al cuerpo de datos de la tabla.
getRowCount() Obtiene el número de filas de la tabla.
getTotalRowRange() Obtiene el objeto de intervalo asociado a la fila de totales de la tabla.
resize(newRange) Cambie el tamaño de la tabla al nuevo intervalo. El nuevo intervalo debe superponerse con el intervalo de tabla original y los encabezados (o la parte superior de la tabla) deben estar en la misma fila.
setName(name) Nombre de la tabla.
Unos ejemplos de esto sería el siguiente código:
function main(workbook: ExcelScript.Workbook) {
let tWb=workbook;
let hoja = tWb.getWorksheet("Tablas");
//creamos nuestra tabla...
let ejemtabla: ExcelScript.Table = hoja.addTable("A1:D1", true /*con encabezados*/);
//le damos nombre
ejemtabla.setName("Mi_Tabla");
//incorporamos lso títulos de los campos
ejemtabla.getHeaderRowRange().setValues([["Fecha", "Producto", "Unidades", "Importe"]]);
//añadimos un conjunto de filas
ejemtabla.addRows(null /*agrega un conjunto de filas al final de la tabla*/,
[
["1/1/2023", "Pdto A", 103, "123.45"],
["2/15/2023", "Pdto B", 22, "987.65"],
["5/21/2023", "Pdto C", 12, "654.02"]
]);
//Añado una nueva columna___________________________________________
//indicamos posición de la nueva columna - null para añadirla al final
//después una matriz que incluya posiciones para encabezados y filas
//y por úlitmo el título para el campo/columna
ejemtabla.addColumn(4,["","1","5","6"],"Descuento")
//Inserto una única fila nueva en la primera posición_________________
//indicamos la posicón de la fila a insertar
//y luego el vector-matriz de datos
ejemtabla.addRow(0,["09/13/2023","Pdto DD",13,"111.11","9"])
//recuperamos los distintos elementos_________________________________
//el encabezado
let encab=ejemtabla.getHeaderRowRange().getValues()
console.log(encab)
//el nombre de la tabla
let nombre=ejemtabla.getName()
console.log(nombre)
//el rango que ocupa toda la tabla
let rngTabla=ejemtabla.getRange().getAddressLocal()
console.log(rngTabla)
//el número de filas de la tabla
let numfilas=ejemtabla.getRowCount()
console.log(numfilas)
//recuperamos una matriz con el contenido solo de la parte de datos
//sin encabezado ni fila de totales
let databody=ejemtabla.getRangeBetweenHeaderAndTotal().getValues()
console.log(databody)
//redimensionamos el tamaño de la tabla,
//dos columnas y tres filas mas
ejemtabla.resize(ejemtabla.getRange().getResizedRange(3, 2).getAddressLocal())
console.log(ejemtabla.getRange().getAddressLocal())
//eliminamos la fila 5 y 6___________________________________________
ejemtabla.deleteRowsAt(4,2)
//eliminamos la tabla____________________________________________
ejemtabla.delete()
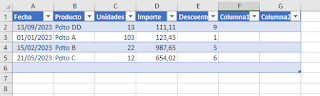
}El resultado previo a eliminar la tabla (último paso) es:
Ten presente que para trabajar a nivel de columnas deberás, en algunas ocasiones, hacer uso del interface ExcelScript.TableColumn!!!
Por suerte los métodos y propiedades en este caso son solo diez ;-)
delete() Elimina la columna de la tabla.
getFilter() Recupera el filtro aplicado a la columna.
getHeaderRowRange() Obtiene el objeto de rango asociado a la fila de encabezado de la columna.
getId() Devuelve una clave única que identifica la columna de la tabla.
getIndex() Devuelve el número de índice de la columna dentro de la colección de columnas de la tabla. Indizado con cero.
getName() Especifica el nombre de la columna de tabla.
getRange() Obtiene el objeto de rango asociado a toda la columna.
getRangeBetweenHeaderAndTotal() Obtiene el objeto de rango asociado al cuerpo de datos de la columna.
getTotalRowRange() Obtiene el objeto de rango asociado a la fila de totales de la columna.
setName(name) Especifica el nombre de la columna de tabla.
Además de los métodos concretos dentro de ExcelScript.Table como pueden ser:
getColumn(key) Obtiene un objeto de columna por nombre o identificador. Si la columna no existe, este método devuelve undefined.
getColumnById(key) Obtiene un objeto de columna por identificador. Si la columna no existe, devolverá undefined.
getColumnByName(key) Obtiene un objeto de columna por Name. Si la columna no existe, devolverá undefined.
getColumns() Representa una colección de todas las columnas de la tabla.
y del ya comentado
addColumn(index, values, name): Agrega una nueva columna a la tabla.
Un ejemplo lo podemos ver en el siguiente código:
function main(workbook: ExcelScript.Workbook) {
let tWb = workbook;
let hoja = tWb.getWorksheet("Tablas");
//definimos una variable que corresponda con nuestra tabla...
let ejemtabla: ExcelScript.Table = hoja.getTables()[0];
console.log (ejemtabla.getName());
//defino una variable de la 'Importe'
let col:ExcelScript.TableColumn = ejemtabla.getColumnByName('Importe');
//recuperamos la posición de la columna
let posicion=col.getId();
console.log(posicion);
//Cambiamos el nombre de la columna
col.setName("Importe_EUR");
//Obtenemos el rango, como string, de celdas correspondiente a la columna
let rango=col.getRangeBetweenHeaderAndTotal().getAddressLocal();
console.log(rango);
//O bien como Array de valores
let arrCol=col.getRangeBetweenHeaderAndTotal().getValues();
console.log(arrCol);
//podríamos tambien eliminar la columna identificada
//col.delete ()
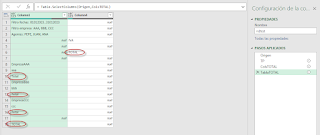
} El efecto del trabajo lo vemos en la imagen siguiente:
Espero sirva como breve introducción al trabajo con tablas en nuestras hojas de cálculo con Office Scripts.