Sabemos de las bondades de las funciones matriciales en Excel, y de las altas posibilidades que nos otorgan si tenemos los suficientes recursos para configurarlas.
En varias entradas anteriores del blog he explicado las dos grandes maneras de trabajar con las matriciales, a saber: Trabajar sobre rangos y obtener un único resultado, y Obtener un rango de resultados.
En el ejercicio de hoy optaremos por la primera opción, esto es, trabajaremos sobre rangos obteniendo un único resultado en una sola celda.
El objetivo de hoy es determinar de un conjunto de registros cuáles están cuadrados y cuales no, basándonos en una condición. En particular disponemos de un listado de movimientos contables de clientes, en los que se detalla registro a registro lo facturado y lo cobrado, todo ello representado (para simplificar) en tres columnas: 'Cliente' 'Debe' y 'Haber'.
Para los no iniciados en conceptos contables, los apuntes en el 'Debe' representan las cantidades facturadas y los apuntes en el 'Haber' los importes cobrados. Lógicamente todo lo facturado deberá coincidir con lo cobrado ( y viceversa).
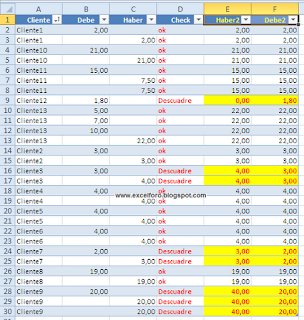
Vemos la tabla de registros desordenados en un principio y que, posteriormente ordenaremos por 'Cliente' para visualizar mejor el concepto a conseguir:
Para comprobar si todo importe facturado por un cliente tiene su correspondiente importe cobrado (o viceversa), lo primero que haremos será convertir en una Tabla nuestro listado de trabajo. Para ello seleccionamos el rango A1:C30 y desde la ficha Insertar > Tablas > Tabla, o bien presionamos Ctrl+t.
Convertir el rango de datos en Tabla es únicamente para facilitar la posterior incorporación de nuestra fórmula matricial para cada registro de la tabla, ya que, recuerdo, la fórmula matricial trabaja sobre rangos y devuelve el resultado en una sóla celda.
Con la Tabla creada incorporaremos una nueva columna que llamaremos 'Check', donde incluiremos la fórmula matricial que nos dirá si ese registro tiene su contrapartida o no:
Y llegamos por fin a la matricial buscada que introducimos en la celda D2:
=SI(SUMA(VALOR(([Cliente]=A2)*[Haber]))=SUMA(VALOR(([Cliente]=A2)*[Debe]));"ok";"Descuadre")
ojo con la notación especial de las Tablas!!. No olvidemos validarla presionando Ctrl+Mayusc+Enter. Al hacerlo, y ser la celda D2 parte de la columna de una tabla, se autorrellenará para cada elemento (este era el motivo de convertir en Tabla el rango).
Para comprobar visualmente que la fórmula funciona correctamente, y antes de explicar el desarrollo de nuestra matricial, ordenamos nuestra Tabla por el campo 'Cliente':
Se observa fácilmente como para aquellos grupos de clientes que no suma lo mismo el 'Debe' que el 'Haber' obtenemos un Descuadre; es decir, se verifica para cada Cliente que todas las partidas del 'Debe' (facturadas) se corresponden con todas las partidas del 'Haber' (cobradas); comprobando por tanto cuáles están cuadradas/conciliadas y cuáles no.
El funcionamiento de la fórmula matricial:
=SI(SUMA(VALOR(([Cliente]=A2)*[Haber]))=SUMA(VALOR(([Cliente]=A2)*[Debe]));"ok";"Descuadre")
es sencillo. Obtenemos una suma del rango de valores del 'Haber' por cliente:
SUMA(VALOR(([Cliente]=A2)*[Haber]))
y verificamos que sumando los valores correspondientes de ese cliente del 'Debe'
SUMA(VALOR(([Cliente]=A2)*[Debe]))
llegamos a la misma cantidad, señal que todo lo cobrado es igual a lo facturado, i.e., que está conciliado.
Podemos ver en la imagen el rango que obtendríamos correpondiente con el cliente situado en A2 para la columna del Debe y del Haber:
Sólo en los casos que esa suma parcial por cliente concreto sea igual en ambas columnas significaría partidas cuadradas o conciliadas.
He tenido que anidar el rango ([Cliente]=A2)*[Debe]) y ([Cliente]=A2)*[Haber]) como argumento de la función VALOR, para convertir el resultado en valores numéricos operables, ya que en ocasiones, al trabajar con matriciales, y más cuando uno de los rangos es tipo texto, el resultado obtenido es tipo texto, esto es, no operable; por lo que la SUMA posteior no nos devolvería ningún resultado.
En varias entradas anteriores del blog he explicado las dos grandes maneras de trabajar con las matriciales, a saber: Trabajar sobre rangos y obtener un único resultado, y Obtener un rango de resultados.
En el ejercicio de hoy optaremos por la primera opción, esto es, trabajaremos sobre rangos obteniendo un único resultado en una sola celda.
El objetivo de hoy es determinar de un conjunto de registros cuáles están cuadrados y cuales no, basándonos en una condición. En particular disponemos de un listado de movimientos contables de clientes, en los que se detalla registro a registro lo facturado y lo cobrado, todo ello representado (para simplificar) en tres columnas: 'Cliente' 'Debe' y 'Haber'.
Para los no iniciados en conceptos contables, los apuntes en el 'Debe' representan las cantidades facturadas y los apuntes en el 'Haber' los importes cobrados. Lógicamente todo lo facturado deberá coincidir con lo cobrado ( y viceversa).
Vemos la tabla de registros desordenados en un principio y que, posteriormente ordenaremos por 'Cliente' para visualizar mejor el concepto a conseguir:
Para comprobar si todo importe facturado por un cliente tiene su correspondiente importe cobrado (o viceversa), lo primero que haremos será convertir en una Tabla nuestro listado de trabajo. Para ello seleccionamos el rango A1:C30 y desde la ficha Insertar > Tablas > Tabla, o bien presionamos Ctrl+t.
Convertir el rango de datos en Tabla es únicamente para facilitar la posterior incorporación de nuestra fórmula matricial para cada registro de la tabla, ya que, recuerdo, la fórmula matricial trabaja sobre rangos y devuelve el resultado en una sóla celda.
Con la Tabla creada incorporaremos una nueva columna que llamaremos 'Check', donde incluiremos la fórmula matricial que nos dirá si ese registro tiene su contrapartida o no:
Y llegamos por fin a la matricial buscada que introducimos en la celda D2:
=SI(SUMA(VALOR(([Cliente]=A2)*[Haber]))=SUMA(VALOR(([Cliente]=A2)*[Debe]));"ok";"Descuadre")
ojo con la notación especial de las Tablas!!. No olvidemos validarla presionando Ctrl+Mayusc+Enter. Al hacerlo, y ser la celda D2 parte de la columna de una tabla, se autorrellenará para cada elemento (este era el motivo de convertir en Tabla el rango).
Para comprobar visualmente que la fórmula funciona correctamente, y antes de explicar el desarrollo de nuestra matricial, ordenamos nuestra Tabla por el campo 'Cliente':
Se observa fácilmente como para aquellos grupos de clientes que no suma lo mismo el 'Debe' que el 'Haber' obtenemos un Descuadre; es decir, se verifica para cada Cliente que todas las partidas del 'Debe' (facturadas) se corresponden con todas las partidas del 'Haber' (cobradas); comprobando por tanto cuáles están cuadradas/conciliadas y cuáles no.
El funcionamiento de la fórmula matricial:
=SI(SUMA(VALOR(([Cliente]=A2)*[Haber]))=SUMA(VALOR(([Cliente]=A2)*[Debe]));"ok";"Descuadre")
es sencillo. Obtenemos una suma del rango de valores del 'Haber' por cliente:
SUMA(VALOR(([Cliente]=A2)*[Haber]))
y verificamos que sumando los valores correspondientes de ese cliente del 'Debe'
SUMA(VALOR(([Cliente]=A2)*[Debe]))
llegamos a la misma cantidad, señal que todo lo cobrado es igual a lo facturado, i.e., que está conciliado.
Podemos ver en la imagen el rango que obtendríamos correpondiente con el cliente situado en A2 para la columna del Debe y del Haber:
Sólo en los casos que esa suma parcial por cliente concreto sea igual en ambas columnas significaría partidas cuadradas o conciliadas.
He tenido que anidar el rango ([Cliente]=A2)*[Debe]) y ([Cliente]=A2)*[Haber]) como argumento de la función VALOR, para convertir el resultado en valores numéricos operables, ya que en ocasiones, al trabajar con matriciales, y más cuando uno de los rangos es tipo texto, el resultado obtenido es tipo texto, esto es, no operable; por lo que la SUMA posteior no nos devolvería ningún resultado.






=SI(SUMA(VALOR(([Cliente]=A2)*[Haber]))=SUMA(VALOR(([Cliente]=A2)*[Debe]));"ok";"Descuadre")
ResponderEliminarNo funciona... todos los resultados son Descuadre.
¿son correctas todas las funciones utilizadas?
gracias
Hola,
Eliminarsi son correctas; debes aplicar la fórmula matricialmente, como se indica en la entrada, esto es, presionando Ctrl+Mayusc+Enter...
en caso contrario, te ocurre lo que comentas.
Slds
Exclente aportacion. una pregunta y como se le haria para consolidar varios registros de un cliente, por ejemplo:
ResponderEliminarCLIENTE No..1. DEBE ....... HABER
REGISTRO A) 2,000 ....... 2,800
REGISTRO B) 500
REGISTRO C) 300
Agradeceria su aportacion al respecto.
Saludos
Ezequiel Sanchez
Hola Ezequiel,
Eliminareste mismo modelo considera diferentes registros de un mismo cliente, si te fijas en los clientes 9, 11 y 13, tienes más de dos.
Saludos