Algo de geometría divertida (y práctica).
Planteamos en el post del día la forma de conseguir en un gráfico polígonos concéntricos.
Comenzaremos con el planteamiento de un pentágono.
Para tal fin emplearemos el tipo de gráfico de Dispersión con Líneas Rectas.
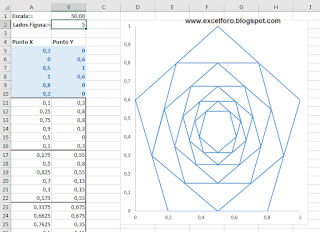
De vital importancia será la distribución inicial de puntos que realicemos (en la imagen anterior el rango en azul: A5:B10).
Como podemos notar para completar el polígono elegido debemos distribuir el par ordenado de cada punto, completando la figura.
Siempre un punto más que los vértices del polígono, que es el punto de partida!!!.
En nuestro ejemplo de un pentágono tenemos los seis puntos:
0,2 - 0
0 - 0,6
0,5 - 1
1 - 0,6
0,8 - 0
0,2 - 0
Primero y último coincidentes.
Por otro lado disponemos de un factor de corrección para conseguir el efecto 'concéntrico', el efecto de insertar uno dentro de otro exactamente... Este factor lo añadimos en la celda B1.
Por otra parte, para poder aprovechar nuestras fórmulas para otros polígonos, disponemos de otra celda B2 donde indicamos los lados de nuestro polígono...
Construimos nuestra secuencia de puntos. Podemos añadir tantos como deseemos; por tanto, a mayor número de puntos para nuestra serie, mayor número de polígonos (pentágonos) se reflejarán en el gráfico.
En nuestra celda A11 incluimos la siguiente fórmula (para luego arrastrar hacia abajo):
=SI(MULTIPLO.INFERIOR.MAT(CONTAR($A$5:A10)+1;$B$2+1)=CONTAR($A$5:A10)+1;DESREF(A11;-$B$2;0);A5-(A5-A6)*$B$1/100)
En B11 añadimos (para luego arrastrar hacia abajo):
=SI(MULTIPLO.INFERIOR.MAT(CONTAR($B$5:B10)+1;$B$2+1)=CONTAR($B$5:B10)+1;DESREF(B11;-$B$2;0);B5-(B5-B6)*$B$1/100)
la cuales aseguran que el pentágono se cierra para cada tramo de seis puntos.
Se observa en las filas 11 y 16, o 17 y 22 en la imagen del inicio...
Finalmente seleccionamos el rango con los datos calculados A4:B52 en mi ejemplo y sobre el insertamos el gráfico de Dispersión con Líneas Rectas.
Eliminamos leyenda y título, así como líneas de división. Si fuera necesario ajustamos en las Opciones de los ejes el escalado de éstos.
LLegando finalmente a nuestro gráfico buscado:
Otro polígono podría ser el octógono (ocho lados), cuya distribución en puntos (nueve, i.e., 8 + 1) del primero de ellos podría ser:
0,33 - 0
0 - 0,33
0 - 0,66
0,33 - 1
0,66 - 1
1 - 0,66
1 - 0,33
0,66 - 0
0,33 - 0
Como vemos en la imagen siguiente:
Las fórmulas son las mismas, pero adaptadas al rango inicial A5:B13...
Planteamos en el post del día la forma de conseguir en un gráfico polígonos concéntricos.
Comenzaremos con el planteamiento de un pentágono.
Para tal fin emplearemos el tipo de gráfico de Dispersión con Líneas Rectas.
De vital importancia será la distribución inicial de puntos que realicemos (en la imagen anterior el rango en azul: A5:B10).
Como podemos notar para completar el polígono elegido debemos distribuir el par ordenado de cada punto, completando la figura.
Siempre un punto más que los vértices del polígono, que es el punto de partida!!!.
En nuestro ejemplo de un pentágono tenemos los seis puntos:
0,2 - 0
0 - 0,6
0,5 - 1
1 - 0,6
0,8 - 0
0,2 - 0
Primero y último coincidentes.
Por otro lado disponemos de un factor de corrección para conseguir el efecto 'concéntrico', el efecto de insertar uno dentro de otro exactamente... Este factor lo añadimos en la celda B1.
Por otra parte, para poder aprovechar nuestras fórmulas para otros polígonos, disponemos de otra celda B2 donde indicamos los lados de nuestro polígono...
Construimos nuestra secuencia de puntos. Podemos añadir tantos como deseemos; por tanto, a mayor número de puntos para nuestra serie, mayor número de polígonos (pentágonos) se reflejarán en el gráfico.
En nuestra celda A11 incluimos la siguiente fórmula (para luego arrastrar hacia abajo):
=SI(MULTIPLO.INFERIOR.MAT(CONTAR($A$5:A10)+1;$B$2+1)=CONTAR($A$5:A10)+1;DESREF(A11;-$B$2;0);A5-(A5-A6)*$B$1/100)
En B11 añadimos (para luego arrastrar hacia abajo):
=SI(MULTIPLO.INFERIOR.MAT(CONTAR($B$5:B10)+1;$B$2+1)=CONTAR($B$5:B10)+1;DESREF(B11;-$B$2;0);B5-(B5-B6)*$B$1/100)
la cuales aseguran que el pentágono se cierra para cada tramo de seis puntos.
Se observa en las filas 11 y 16, o 17 y 22 en la imagen del inicio...
Finalmente seleccionamos el rango con los datos calculados A4:B52 en mi ejemplo y sobre el insertamos el gráfico de Dispersión con Líneas Rectas.
Eliminamos leyenda y título, así como líneas de división. Si fuera necesario ajustamos en las Opciones de los ejes el escalado de éstos.
LLegando finalmente a nuestro gráfico buscado:
Otro polígono podría ser el octógono (ocho lados), cuya distribución en puntos (nueve, i.e., 8 + 1) del primero de ellos podría ser:
0,33 - 0
0 - 0,33
0 - 0,66
0,33 - 1
0,66 - 1
1 - 0,66
1 - 0,33
0,66 - 0
0,33 - 0
Como vemos en la imagen siguiente:
Las fórmulas son las mismas, pero adaptadas al rango inicial A5:B13...




No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.