En algunas entradas anteriores del blog hemos hecho uso de propiedades binarias para conseguir nuestras metas, por eso analizaremos hoy el 'mundo' binario en Excel.
Es interesante abordar una breve lectura en Wikipedia.
Comenzaremos revisando la función de Excel específica para convertir un número decimal a binario:
=DEC.A.BIN((número, [caracteres])
dos argumentos, el número decimal a convertir y opcionalmente con cuantos caracteres queremos mostrarlos.
Esta es una función bien simple de emplear pero con una gran limitación.. y es que solo permite números decimales entre -512 y 511 !!!
Sin duda muy corto en la mayoría de los casos...
Por este motivo desarrollaremos algunos de los métodos rutinarios para obtener los necesitados números binarios, salvando esa limitación.
Como primera alternativa veremos la clásica división por dos y con el residuo o resto de esas divisiones (que serán 0 y 1) compondremos nuestro binario.
El método descrito se detalla dividiendo el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2, esstoes, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordena desde el último cociente hasta el primer resto, simplemente se colocan en orden inverso a como aparecen en la división. Este será el número binario que buscamos.
Podríamos replicarlos manualmente con fórmulas, pero parece más interesante montar una función personalizada con programación que realice el cálculo.
Así pues insertamos el código VBA en un módulo estándar del editor de VB:
Es interesante abordar una breve lectura en Wikipedia.
Comenzaremos revisando la función de Excel específica para convertir un número decimal a binario:
=DEC.A.BIN((número, [caracteres])
dos argumentos, el número decimal a convertir y opcionalmente con cuantos caracteres queremos mostrarlos.
Esta es una función bien simple de emplear pero con una gran limitación.. y es que solo permite números decimales entre -512 y 511 !!!
Sin duda muy corto en la mayoría de los casos...
Por este motivo desarrollaremos algunos de los métodos rutinarios para obtener los necesitados números binarios, salvando esa limitación.
Como primera alternativa veremos la clásica división por dos y con el residuo o resto de esas divisiones (que serán 0 y 1) compondremos nuestro binario.
El método descrito se detalla dividiendo el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2, esstoes, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordena desde el último cociente hasta el primer resto, simplemente se colocan en orden inverso a como aparecen en la división. Este será el número binario que buscamos.
Podríamos replicarlos manualmente con fórmulas, pero parece más interesante montar una función personalizada con programación que realice el cálculo.
Así pues insertamos el código VBA en un módulo estándar del editor de VB:
Function NumBIN(NumDecimal As Range)
'OJO!!! valor max 1.999.999.999 y positivos
'Método ... dividiendo por dos
Dim digitos() As Long
'cuantos dígitos necesitaremos para convertirloa binario
n = 0
Do
n = n + 1
rdo = NumDecimal ^ (1 / n)
Loop Until rdo < 2
'redefinimos la matriz para cargar cada dígito binario
ReDim digitos(1 To n) As Long
'hacemos las divisiones necesarias y
'cargamos nuestra matriz de dígitos....
div = NumDecimal
For dig = 1 To n
digitos(dig) = div Mod 2 'residuo o resto de la división entre 2
div = div \ 2 'división entera !!
Next dig
'componemos nuestro numero binario
For i = 1 To n
txt = digitos(i) & txt
Next i
'y lo devolvemos a la función
NumBIN = txt
End Function
La limitación de esta función ahora la encontramos en el número decimal 1.999.999.999 y en que siempre deben ser números positivos!!.
Una segunda alternativa es empleando funciones en nuestra hoja de cálculo.
Si revisamos la imagen del inicio del post, en la celda D6 para tratar el número decimal de la celda B6 escribíamos:
=DEC.A.BIN(RESIDUO(COCIENTE($B$6;256^5);256);8)&
DEC.A.BIN(RESIDUO(COCIENTE($B$6;256^4);256);8)&
DEC.A.BIN(RESIDUO(COCIENTE($B$6;256^3);256);8)&
DEC.A.BIN(RESIDUO(COCIENTE($B$6;256^2);256);8)&
DEC.A.BIN(RESIDUO(COCIENTE($B$6;256^1);256);8)&
DEC.A.BIN(RESIDUO(COCIENTE($B$6;256^0);256);8)
Como se observa partimos en 6 partes o tramos el número a convertir, componiendo una secuencia de concatenados como múltiplos de 256, retornando 'paquetes' de ocho caracteres secuenciados... para una vez divididos y con el resto del cociente recuperado, pasar éste último a su forma binaria con la función DEC.A.BIN
Es una forma curiosa que encontré en un foro (no puedo recordar dónde) aunque desarrollada de una manera algo mas simple...
Tiene como límite el decimal cercano a: 287.000.000.000
Y una tercera alternativa será empleando el método de distribución.Este método consiste en distribuir los 1 necesarios entre las potencias sucesivas de 2 de modo que su suma resulte ser el número decimal a convertir.
Por ejemplo el número 131, para el que se necesitarán las 8 primeras potencias de 2, ya que la siguiente, 28=256, es superior al número a convertir.Se comienza poniendo un 1 en 128, por lo que aún faltarán 3, 131-128 = 3, para llegar al 131.Este valor se conseguirá distribuyendo unos entre las potencias cuya suma dé el resultado buscado y poniendo ceros en el resto.
En nuestro caso resultan ser las potencias 1 y 0, esto es,2 y 1, respectivamente.
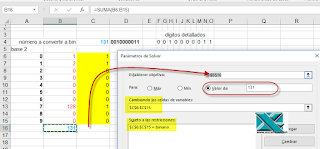
Para replicar este modelo emplearemos Solver.Al montar nuestro modelo, llevaremos números naturales de 0 a 9 (en este caso) en las celdas A6:A15 (serán las potencias a aplciar a nuestra base 2...Lo que generamos en el rango de celdas B6:B15 con la fórmula:=C6*2^A6
observa que a la potencia2^A6la multiplicamos por las celdas C6:C15 que Solver se encargará de completar con 0 y 1 hasta conseguir que la suma de B5:B15 sea igual al decimal buscado... Es decir, nuestras celda objetivo en Solver es B16 que contiene la función=SUMA(B6:B15)
Estamos listos para configurar Solver, así en la ventana de configuración:
Las celdas cambiantes serán las del rango C5:C15.. las mismas a las que hemos agregado la condición que sena binarias, esto es, que sean 0 y 1...
Al lanzar Solver comprobaremos como logra calcular la combinación de 0 y 1 para sumar el 131 buscado.



Hola, un artículo muy interesante. Tengo una duda, he estado hasta ahora usando un traductor para binario https://traductorbinario.online/ (ahora usare esta tabla de excel) ¿Podría decirme cuanto de fiable son estos treaductores?
ResponderEliminarHola Diego,
Eliminarno sabría darte un porcentaje... pero este método, las veces que lo he empleado ha sido 100% fiable...
Pero ya sabes que la certidumbre absoluta no existe ..
Slds